Get Started with NeuroLang¶

First Steps With NeuroLang¶

NeuroLang is a unifying formalism to perform complex queries and explorations using heterogeneous data sources like tabular data, volumetric images, and ontologies. To perform this in sound manner, NeuroLang is a probabilistic logic programming language based on Datalog [abiteboul1995], [maier2018].

The whole idea of logic programming is to be able to make assertions of the style:

region x is a left hemisphere gyrus if the label of x in Destrieux et al’s atlas starts with “L G”.

which can be formalised in first order logic as

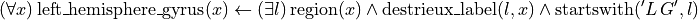
$(\forall x) \operatorname{left\_hemisphere\_gyrus}(x) \leftarrow (\exists l) \operatorname{region}(x) \wedge \operatorname{destrieux\_label}(l, x) \wedge \operatorname{startswith}('L\, G', l)$

which, if we assume that 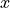$x$ being on Destrieux et al’s atlas means that 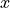$x$ is already a region, can be shortened as

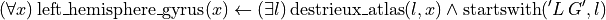
$(\forall x) \operatorname{left\_hemisphere\_gyrus}(x) \leftarrow (\exists l) \operatorname{destrieux\_atlas}(l, x) \wedge \operatorname{startswith}('L\,G', l)$

Finally, for notation convenience, we will drop the quantifiers, assuming that all variable on the left of the arrow (such as 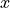$x$ ) is universally quantified, and all variable appearing only on the right of the arrow (such as 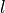$l$ ) will be existentially quantified [maier2018]. This leads to the expression

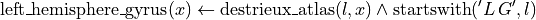
$\operatorname{left\_hemisphere\_gyrus}(x) \leftarrow \operatorname{destrieux\_atlas}(l, x) \wedge \operatorname{startswith}('L\,G', l)$

which we formalise in python as:

with neurolang.scope as e:
    e.left_hemisphere_gyrus[e.x] = e.destrieux_atlas(e.l, e.x) & e.startswith('L G', e.l)

the full example is in our gallery in Loading and Querying the Destrieux et al. Atlas’ Left Hemisphere.

Negation can also be used in Neurolang. For instance

Disjunctions in Logic Programming¶

Disjunctions in logic programming merit are a very specific case. For instance, let’s say that all the regions in the left hemisphere’s cortex are either a sulcus or gyrus, or more specifically

x is a left hemisphere region if x is left sulcus or x is left gyrus

which in first order logic can be formalised as

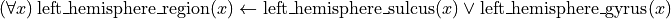
$(\forall x)\operatorname{left\_hemisphere\_region}(x) \leftarrow \operatorname{left\_hemisphere\_sulcus}(x) \vee \operatorname{left\_hemisphere\_gyrus}(x)$

alternatively, this can be written as a set of two propositions

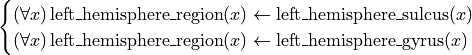
$\begin{cases} (\forall x)\operatorname{left\_hemisphere\_region}(x) \leftarrow \operatorname{left\_hemisphere\_sulcus}(x)\\ (\forall x)\operatorname{left\_hemisphere\_region}(x) \leftarrow \operatorname{left\_hemisphere\_gyrus}(x) \end{cases}$

which we formalise in Neurlang in the classical logical programming syntax:

with neurolang.scope as e:
    e.left_hemisphere_region[e.x] = e.left_hemisphere_sulcus(x)
    e.left_hemisphere_region[e.x] = e.left_hemisphere_gyrus(x)

or in a less verbose manner:

with neurolang.scope as e:
    e.left_hemisphere_region[e.x] = e.left_hemisphere_sulcus(e.x) | e.left_hemisphere_gyrus(e.x)

Aggregations¶

Aggregations combine information from a set of tuples. A good example of an aggregation is the maximum. As a mathematical definition we could define an aggregation as

$\begin{split} (\forall country)\operatorname{max\_population\_per\_country}\left(country, max(\{pop: (\exists province)\operatorname{population\_per\_country\_province}(country, province, pop)\})\right) \leftarrow \\ (\exists province)(\exists pop)\operatorname{population\_per\_country\_province}(country, province, pop) \end{split}$

which in neurolang is expressed as

with neurolang.scope as e:
    e.max_population_per_country[e.country, e.max(e.pop)] = e.population_per_country_province(e.country, e.province, e.pop)

[abiteboul1995]

Abiteboul, S., Hull, R. & Vianu, V. Foundations of databases. (Addison Wesley, 1995).

[maier2018] (1,2)

Maier, D., Tekle, K. T., Kifer, M. & Warren, D. S. Datalog: concepts, history, and outlook. in Declarative Logic Programming (eds. Kifer, M. & Liu, Y. A.) 3–100 (Association for Computing Machinery and Morgan & Claypool, 2018). doi:10.1145/3191315.3191317.